前ページで述べた計算機実験結果から,信号周期T が短くなると(角速度ω が大きくなると) 車両の平均速度は大きくなり,この傾向はオフセット制御の方法に依存しないことがわかった.
たとえばT=1.0[sec] のような極端に短い信号周期は実用に供するのが不可能なため,考察の対象外とし,実用的な値の周期を用いた場合の可変角速度位相振動子系によるオフセット制御の有効性を前節までで示したわけであるが,上記のような信号周期と平均速度との相関関係は,それ自身として興味深い事実であり,その本質を考察しておく意義があると考える.
本ページでは,その考察を行ない,計算機実験により,その妥当性を検証する.
まず,信号周期と車両の平均速度との関係について,次のような推測を行なった.
すなわち,本研究で行なったシミュレーションでは,全車両は制限速度を目標値として加速し,赤信号で減速して,停止する.一般に交差点での停止回数と待ち時間の積が街路網を通過する走行時間(平均旅行時間) を増加させ,それにほぼ反比例する平均速度を低下させる.
本実験では,スプリット(信号周期中の主道路の青信号時間の割合) は一定としているから,交差点での停止確率は信号周期に依存しない.
一方,待ち時間は信号周期に比例するため,信号周期が短くなると交差点での待ち時間が減少し,結果として平均速度が向上するものと考えられる.
以上の推測の妥当性を検証するため,以下のような計算機実験を行なった.
ここでは,信号周期の影響のみを調べるため,位相振動子系を用いた微細なオフセット制御は行わず,同時型(位相差0) と交互型(位相差π)の固定オフセットのみを用いた.
その他の設定は全ページに述べたとおりにし,角速度を0:104[rad/sec]~1:047[rad/sec](信号周期6:0[sec]) まで変化させた場合の平均待ち時間の変化を測定した.
ここで,平均待ち時間は次のように定義し,算出した.
すなわち,対象道路網に車両が進入してから退出するまでの間で,走行速度が零であった時間の総和を各車両の待ち時間とし,走行した全車両に対するその平均値を平均待ち時間とした.
実験結果を下記の図 に示す.
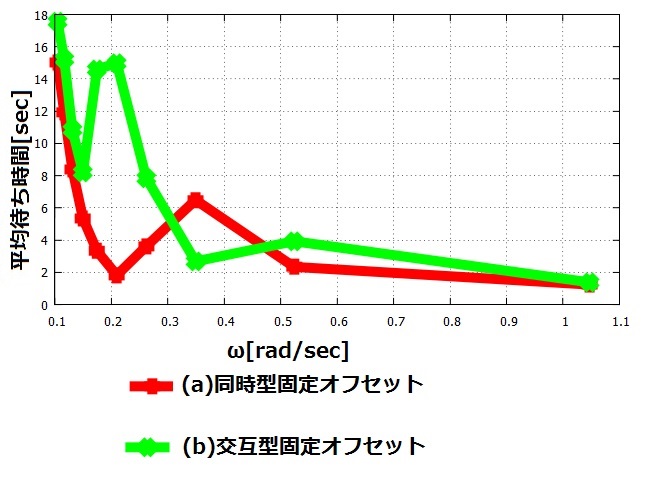
この図から,同時型オフセットと交互型オフセットで制御したいずれの場合も,角速度が大きくなる(信号周期が短くなる) につれて平均待ち時間が減少していることがわかり,上記の推測の妥当性が確認できたと言える.
なお,両者の値が交互に変動しているのは次のように説明される.
すなわち,本実験での平均待ち時間は各交差点での車両の待ち時間ではなく,車両が街路網内に滞在する間の待ち時間の総和と定義しているため,交差点での停止回数が多いほど,平均待ち時間は長くなる.
交差点での停止回数はオフセットに影響され,また同時型と交互型の固定オフセット制御の効果は信号周期に左右されるため,図のような変動が生じたものと考えられる.








